Bazat e matematikës: Rëndësia e Logjikës
Apeli i Daniele Gouthier për mësuesit për të ndihmuar fëmijët të kuptojnë lidhjen e pazgjidhshme midis logjikës, matematikës dhe mendimit racional.
Nëse nuk e kërkojmë kuptimin e matematikës, e mësojmë dhe e mësojmë më keq. Ose më keq akoma, nuk e mësojmë dhe nuk e mësojmë fare.
BAZAT E MENDIMIT
Një ndjenjë që unë personalisht e shoh në matematikë është edukimi në abstraksion dhe të menduarit racional. Mendimi racional është ai mendim që di të nxjerrë pasoja nga premisat, duke nxjerrë gjithçka që mund të deduktohet dhe asgjë më shumë.
Ofroni nxënësve tuaj këto tre shembuj, duke i bërë ata të punojnë në grupe të vogla për rreth njëzet minuta.
Të gjithë njerëzit janë të vdekshëm.
Të gjithë evropianët janë burra.
Pra, të gjithë evropianët janë të vdekshëm.
Të gjithë rombët kanë anët paralele.
Të gjithë katrorët kanë rombe.
Pra, të gjithë katrorët kanë brinjë paralele.
Të gjithë shumëfishat e 4 janë çift.
Të gjitha shumëfishat e 20 janë shumëfisha të 4.
Pra, të gjithë shumëfishat e 20 janë çift.
Në këtë pikë pyetini nëse janë të treja të vërteta. Nëse rreshti i tretë i secilit shton diçka ose nëse mund ta shkruante vetë duke filluar nga dy rreshtat e parë. Por mbi të gjitha, pyesni ata se çfarë kanë të përbashkët të katër shembujt. Lërini të argumentojnë, eksperimentojnë, hedhin poshtë.
Nuk ka rëndësi që thonë gjërat “e duhura”, e rëndësishme është që ata të arsyetojnë rreth këtyre katër shembujve.
Le të ndalemi pak në të katërtën, atë të claffi, pirzi dhe koos. Çfarë thotë ai? Une nuk e di! Unë personalisht nuk e kuptoj kuptimin e saj. Por e kuptoj si e thotë. E kuptoj strukturën, logjikën e saj. Logjika është tërësia e marrëdhënieve që “karakterizojnë vetë strukturën e mendimit”, përtej asaj që do të thotë apo jo mendimi.
Le të shohim se çfarë logjike është me një problem që është i përshtatshëm edhe për fëmijët.
Këto karta janë të ngjyrosura në njërën anë dhe kanë një zanore në anën tjetër.
Carlo thotë “Nëse një kartë është e kuqe, atëherë ka një ‘A’ në anën tjetër”.
Për të verifikuar nëse Carlo po thotë të vërtetën, cilat letra duhet të kthejmë? (Duam të gjuajmë sa më pak).

Edhe këtu ka shumë kuptim që të lini diskutimin të zhvillohet për rreth dhjetë minuta në të gjithë klasën ose, nëse kushtet lejojnë, në grupe të vogla.
Përgjigja e saktë është se duhet të kthehen tre letra: e kuqja, “E” dhe “O”.
E kuqe sepse duhet të verifikojmë nënkuptimin e drejtpërdrejtë “Nëse pjesa e pasme është e kuqe, pjesa e përparme ka një A”. Dy të tjerat sepse duhet të testojmë nënkuptimin e kundërt «Nëse pjesa e përparme nuk ka një A, pjesa e pasme nuk është e kuqe». Janë përgjigjet e këtyre dy pyetjeve të cilat së bashku na tregojnë nëse Carlo thotë të vërtetën apo jo.
Mekanizmat logjikë që kemi parë janë të dy llojeve të ndryshme:
Të gjitha B-të janë A. Të gjitha C-të janë B. Pra të gjitha C-të janë A.
Silogjizmi i Logjikës
Nëse C është B, atëherë ajo që nuk është B nuk është C.
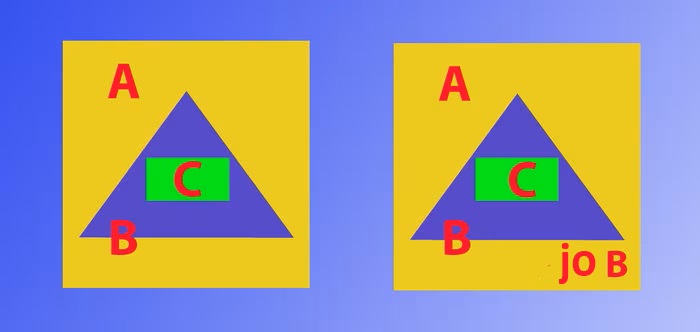
I pari quhet “silogizëm”, i dyti “implikim invers” dhe janë dy mekanizmat logjikë në bazë të deduksioneve tona, demonstrimet e matematikës dhe mendimit racional.
Ia vlen të investoni pak kohë në të që fëmijët dhe të rinjtë të njihen me ta.